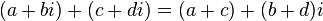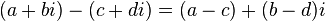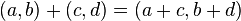وبلاگ تخصصی برق الکترونیک و کنترل

ریاضیات مهندسی


عدد مختلط عددی به شکل  a + ib \, است که a و b اعداد حقیقی‌اند و i یکهٔ موهومی با خصوصیت i2 = -1 است. عدد a قسمت حقیقی و عدد b قسمت موهومی نامیده و نوشته می‌شود:

  • I_mz=b
  • R_ez=a

اعداد حقیقی را می‌توان به عنوان اعداد مختلط با قسمت موهومی صفر در نظر گرفت، یعنی عدد حقیقی a معادل است با عدد مختلط a+0i.

مجموعهٔ اعداد مختلط را بصورت 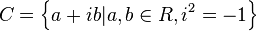C=\left \{a+ib|a, b\in R, i^2=-1\right \}  تعریف می‌کنیم.

 

دانلود فابل آموزشی ریاضیات مهندسی

 

دو عدد مختلط برابرند اگر و تنها اگر بخش‌های حقیقی و موهومی آنها دو به دو با یکدیگر برابر باشند. یعنی a + bi = c + di اگر و تنها اگر a = c و b = d.

نمادگذاری و اعمال جبری

مجموعه اعداد مختلط معمولاً با \mathbb{C} نشان داده می‌شود. اعداد مختلط نیز می‌توانند جمع، تفریق، و ضرب شوند با در نظر گرفتن معادلهٔ i 2 = −1

\,(a + bi) + (c + di) = (a + c) + (b + d)i
\,(a + bi) - (c + di) = (a - c) + (b - d)i
\,(a + bi)(c + di) = ac + bci + adi + bd i^2 = (ac - bd) + (bc + ad)i

تقسیم اعداد مختلط را نیز می‌توان تعریف کرد (پایین را ببینید). بنابراین مجموعه اعداد مختلط یک میدان تشکیل می‌دهد که، در مقایسه با اعداد حقیقی، به طور جبری بسته است.


میدان مختلط

اعداد مختلط را می‌توان به صورت زوج‌های مرتب (a, b) از اعداد حقیقی نیز تعریف کرد. با اعمال:

(a,b) + (c,d) = (a + c,b + d) \,
(a,b) \cdot (c,d) = (ac - bd,bc + ad). \,

بنابراین اعداد مختلط تشکیل یک میدان می‌دهند، میدان مختلط، که با C نشان داده می‌شود. از آنجایی که عدد مختلط a + bi به طور منحصربه‌فرد با یک زوج مرتب (a, b) نمایش داده می‌شود، پس اعداد مختلط یک تناظر یک به یک با نقاط در صفحه دارند. به آن صفحه مختلط گفته می‌شود. عدد حقیقی a را با عدد مختلط (a, 0) نشان می‌دهیم و در این حالت میدان اعداد حقیقی R یک زیرمیدان ازC می‌شود. واحد موهومی i عدد مختلط (0, 1) است. منظوراز تقسیم دو عدد مختلط یعنی \frac{a + ib}{c + id} یافتن عددی است مثل x + iy که در تساوی

a +ib = (c +id ).(x +iy)

صدق نماید، پس از محاسبه رابطه بالا داریم

a +ib = (cx -dy)+i(dx +cy)

پس کافی است اعداد x و y را چنان پیدا کنیم که در روابط

dx + cy = b, cx - dy = a صدق کنند. این دستگاه معادلات یک جواب یکتای زیر را دارد:

x = \frac{ac+bd}{c^{2}+d^{2}} y = \frac{bc-ad}{c^{2}+d^{2}} مگر آنکه c = d = 0 بنابراین \frac{a + ib}{c + id} = \frac{ac+bd}{c^{2}+d^{2}} + i\frac{bc-ad}{c^{2}+d^{2}} البته همین نتیجه را می‌توانستیم از ضرب صورت و مخرج کسر \frac{a + ib}{c + id} در c - id نیز بدست آوریم.

 

دانلود فابل آموزشی ریاضیات مهندسی

imankardanpour دوشنبه 8 اردیبهشت 1393 ساعت 01:44
نظرات 0 + ارسال نظر
برای نمایش آواتار خود در این وبلاگ در سایت Gravatar.com ثبت نام کنید. (راهنما)
ایمیل شما بعد از ثبت نمایش داده نخواهد شد